Auxiliar 4

Cámara e Input

Vicente González

Julieta Coloma

Contexto

Espacios 3D

Para trabajar en tres dimensiones tenemos que tener en cuenta los espacios de nuestros objetos:

Local space

Se corresponden con las coordenadas originales o locales del objeto, se suelen dejar homogéneas para después manipularlas con facilidad.
World space

Corresponde al mundo donde se ubica los objetos, cada objeto tiene una posición, orientación y tamaño en este.
View space

Es el mundo que se esta viendo, por lo tanto, es solo una porción del mundo y esta vinculado a la cámara de la escena
Clip space

Es espacio hómogeneo de OpenGL, desde -1 a 1 en todas las coordenadas, lo que queda fuera se elimina o recorta

Espacios 3D

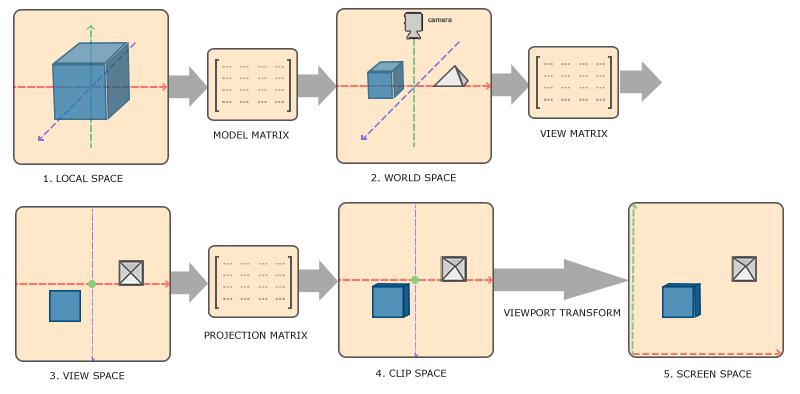
Espacios 3D

Matriz MVP

\[ M_{projection} \cdot M_{view} \cdot M_{model} \cdot v_{local} = v_{clipped} \]

Sirve para moverse desde el espacio local al espacio homogéneo de OpenGL

Modelo

Para pasar de coordenadas locales a las de mundo usamos la matriz de modelo.

\[ M_{model} = M_{translation} \cdot M_{rotation} \cdot M_{scale} \]

Es la que usamos la clase pasada para mover los modelos!

Vista

Para pasar de coordenadas de mundo a las de vista o de cámara, usamos la matriz de vista. Con un poco de magia de álgebra lineal tenemos que:

\[ M_{view} = M_{lookat} = \begin{pmatrix} r_x & r_y & r_z & 0\\ u_x & u_y & u_z & 0\\ d_x & d_y & d_z & 0\\ 0 & 0 & 0 & 1\\ \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 & 0 & -p_x\\ 0 & 1 & 0 & -p_y\\ 0 & 0 & 1 & -p_z\\ 0 & 0 & 0 & 1\\ \end{pmatrix} \]

Donde

\(R\) es el vector que apunta a la derecha de la cámara
\(U\) es el vector que apunta hacia arriba de la cámara
\(D\) es el vector a donde apunta a la cámara
\(P\) es la posición de la cámara

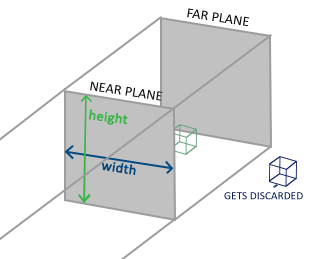
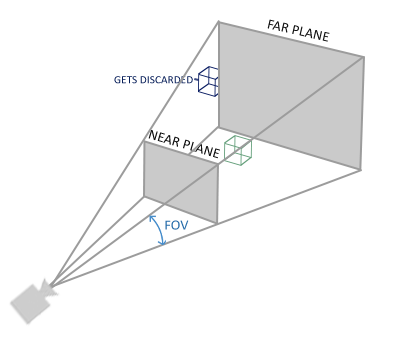
Proyección

Finalmente, para pasar de las coordenadas de vista a las homogéneas de OpenGL se usa la matriz de proyección, que viene en dos sabores:

Ortográfica

def ortho(left, right, bottom, top, near, far)

Perspectiva

def perspective(fovy, aspect, near, far):

Manejo de input

Para manejar input podemos utilizar Pyglet la cual nos provee funciones que son llamadas durante el ciclo del juego, similar a on_draw:

on_key_press(symbol, modifiers): función que se llama cuando se presiona una tecla y se guarda el valor de la tecla en symbol.
on_key_release(symbol, modifiers): función que se llama cuando se libera una tecla y se guarda el valor de la tecla en symbol.
on_mouse_motion(x, y, dx, dy): función que se llama cuando el mouse se mueve y guarda la posición del mouse en la ventana (x e y), así como el cambio de este (dx y dy).

Existen más que pueden ver en la documentación de la librería

Problemas

P1 — Hacerlo con clase

El auxiliar pasado vieron realizar un montón de transformaciones para alterar los modelos, ahora veremos como abstraer el concepto de modelo en una clase.

Una clase es una forma que se tiene para empaquetar código, la idea es que cada clase represente algo.

Cree la clase GameModel, que contenga lo siguiente:

Información de posición, rotación y escalado
Color del objeto y buffer de la GPU
Una función que sea capaz de entregar la matriz de modelo del objeto correspondiente
Una función que sea capaz de dibujar el objeto en pantalla

P1 — Hacerlo con clase

Use esta clase junto a sus nuevos conocimientos para recrear la siguiente escena:

P2 – Hagámoslo FPS

Parte A

Muy bonita su escena pero hay elementos que no se ven completamente, como usted conoce ahora la potente matriz MVP, le gustaría poder moverse en su escena.

Cree la clase Camara que contenga información de la posición de la cámara y su velocidad y use el teclado para moverse en la escena usando on_key_press y on_key_release

P2 – Hagámoslo FPS

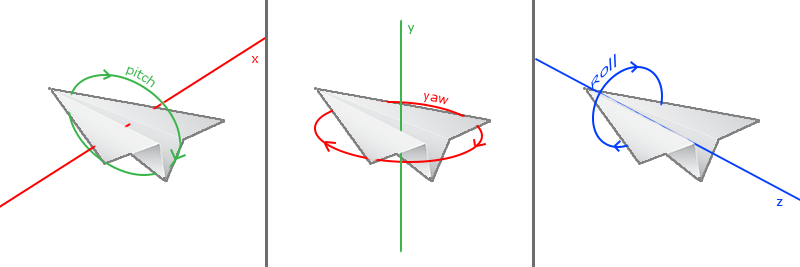
Parte B

Añada los valores de pitch y yaw que permitan mover la cámara, use la función on_mouse_motion para vincular el ángulo de vista con el movimiento del mouse

P2 – Hagámoslo FPS

Parte C

Corrija el movimiento de la parte A para que este sincronizado con la dirección de la cámara

Felicidades! Ahora puedes hacer un 360 no scope 🤠

Fin

Ver otras auxiliares